Let a collection of networks represent interactions within several (social or ecological) systems. Two main issues arise: identifying similarities between the topological structures of the networks or clustering the networks according to the similarities in their structures. We tackle these two questions with a probabilistic model based approach. We propose an extension of the Stochastic Block Model (SBM) adapted to the joint modeling of a collection of networks. The networks in the collection are assumed to be independent realizations of SBMs. The common connectivity structure is imposed through the equality of some parameters. The model parameters are estimated with a variational Expectation-Maximization (EM) algorithm. We derive an ad-hoc penalized likelihood criterion to select the number of blocks and to assess the adequacy of the consensus found between the structures of the different networks. This same criterion can also be used to cluster networks on the basis of their connectivity structure. It thus provides a partition of the collection into subsets of structurally homogeneous networks. The relevance of our proposition is assessed on two collections of ecological networks. First, an application to three stream food webs reveals the homogeneity of their structures and the correspondence between groups of species in different ecosystems playing equivalent ecological roles. Moreover, the joint analysis allows a finer analysis of the structure of smaller networks. Second, we cluster 67 food webs according to their connectivity structures and demonstrate that five mesoscale structures are sufficient to describe this collection.

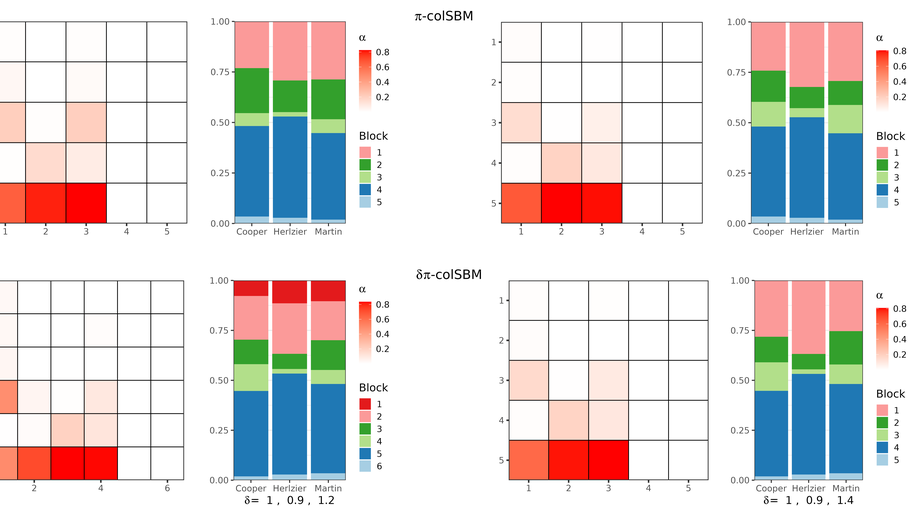
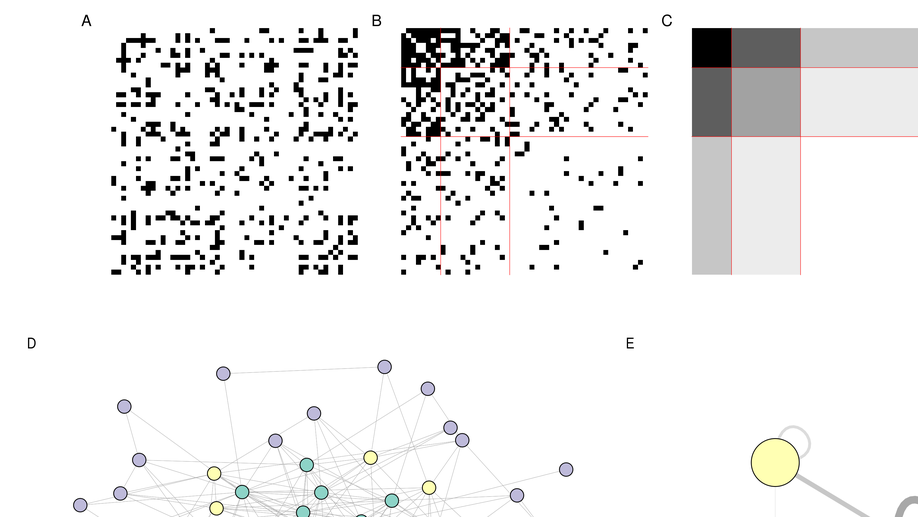
This thesis deals with the development of statistical methods for the analysis of collections of interaction networks through three original contributions. Interaction networks are a natural way to represent in graph form the exchanges or relationships existing between a set of nodes representing species or individuals. Considering collections of networks allows to study heterogeneous systems, composed of several kinds of interactions involving different types of nodes. When the different networks of the collection are linked by a hierarchical relationship, we speak of multilevel networks. The stochastic block model has proven its relevance to model the heterogeneity of the behavior of nodes in a single network. Extensions to collections of networks and to multilevel networks are proposed. They allow to obtain a clustering of the nodes of the networks according to their role in the ecosystem or social system, and to summarize the structure of the system at the mesoscopic scale through a small number of parameters. The inference of these models is complex and variational methods are adapted for this purpose. Model selection methods are also used to determine the dependence between levels for multilevel networks and the similarity between structures for collections of networks.A last part of this thesis proposes a new method to study the robustness of ecological interaction networks. Each network is modeled by a probabilistic model whose parameters represent the network structure. This allows to make the link between the structure of the ecosystem and its robustness, but also to compare the robustness of a collection of networks and to correct the robustness of a network whose sampling would be incomplete.The developed methods are implemented in R packages and applied on data from social sciences and ecology.