A stochastic block model approach for the analysis of multilevel networks: An application to the sociology of organizations
Abstract
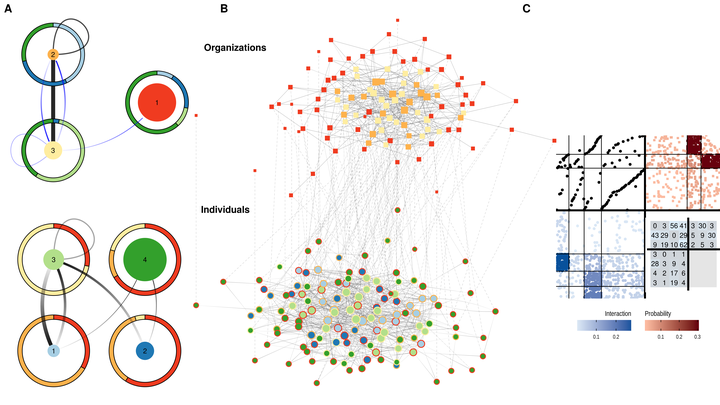
A multilevel network is defined as the junction of two interaction networks, one level representing the interactions between individuals and the other the interactions between organizations. The levels are linked by an affiliation relationship, each individual belonging to a unique organization. A new Stochastic Block Model is proposed as a unified probabilistic framework tailored for multilevel networks. This model contains latent blocks accounting for heterogeneity in the patterns of connection within each level and introducing dependencies between the levels. The sought connection patterns are not specified a priori which makes this approach flexible. Variational methods are used for the model inference and an Integrated Classified Likelihood criterion is developed for choosing the number of blocks and also for deciding whether the two levels are dependent or not. A comprehensive simulation study exhibits the benefit of considering this approach, illustrates the robustness of the clustering and highlights the reliability of the criterion used for model selection. This approach is applied on a sociological dataset collected during a television program trade fair, the inter-organizational level being the economic network between companies and the inter-individual level being the informal network between their representatives. It brings a synthetic representation of the two networks unraveling their intertwined structure and confirms the coopetition at stake.